12th Maths Question Bank: 12-ம் வகுப்பு கணிதப் பாடத்தில் கலக்கல் மதிப்பெண்கள் வேண்டுமா?- இதோ மாதிரி வினாத்தாள்!

12th Maths Model Question Paper: அரசுப் பள்ளி ஆசிரியர்களைக் கொண்டு உருவாக்கிய பொதுத் தேர்வுக்கான 10, 12ஆம் வகுப்பு மாதிரி வினாத்தாள் வங்கியை ABP Nadu சார்பில் தினந்தோறும் வெளியிட்டு வருகிறோம்.

கணித புத்தகம் | கோப்புப்படம்

தமிழ்நாடு முழுவதிலும் இருக்கும் அர்ப்பணிப்பு மிக்க அரசுப் பள்ளி ஆசிரியர்களைக் கொண்டு உருவாக்கிய பொதுத் தேர்வுக்கான 10, 12ஆம் வகுப்பு மாதிரி வினாத்தாள் வங்கியை ABP Nadu சார்பில் தினந்தோறும் வெளியிட்டு வருகிறோம்.

அந்த வகையில் இன்று கணிதப் பாடத்துக்கான மாதிரி வினாத்தாளை இந்தக் கட்டுரையில் காணலாம். 

MODEL QUESTION PAPER-2023

CLASS:         12                                                                                    Total marks:90 Subject: Maths                                                                                                Time : 3.00

Part-I

Answer the all questions:-                                                                 20x1=20

1. If A= 2   3  be such that A^-1=A, the   is  

                  5  -2

a)17                        b)14                                  c)19     d)21

2. If A= 7 3    then 9I-A

                  4  2      

a)A^-1                                b) A^-1/2                             c)3 A^-1                                            d)2 A^-1

3. iⁿ +iⁿ⁺¹+iⁿ⁺²+iⁿ⁺³ is

a)0                          b)1                                    c)-1                             d)i

4. if |z|=1, then the value 1+z is  a)z      b) z-             c) 1/z          d) 1

                                             1+z

5. A zero of x³+64 is a) 0                 b) 4                 c)4i                      d)-4
6. If x= 1/5 the value of cos (Cos^-1x+2sin^-1x) is
7. a) -√24/25 b) √24/25 c) 1/5                          d)-1/5
8. The equation tan^-1x=tan^-1(1/√3) has                                                                                                                                            a) no solution  b) unique solution                  c) two solutions  d) infinite number of solutions.
9. If x+y=k is a number to the parabola y²=12x then the value of k is

a)3                          b)-1                                   c)1                                  d)9

9. Area of the greatest rectangle inscribed in the ellipse x²/a² + y²/b² = 1 is                                                                                      a)2ab b) ab                                 c) √ab                    d) a/b   
10.  If a . b = b . c = c .  a  =0 then the value of [  a ,  b  , c  ] a) |a| |b|  |c|            b) 1/3 |a|   |b|   |c|               c) 1                        d) -1
11. If the direction Cosines of a line are 1/c,1/c,1/c then

a)c=±3                    b)c=±√3                            c) c>0                         d) 0<c<1

12. Angle between y² =x and x² =y at the origin tan^-1 ¾ b) tan^-1 4/3                        c) π/2                     d) π/4                               
13. the point of inflection of the curve y=(x-1)³ a) (0,0) b) (0,1)                             c) (1,0)                  d) (1,1)
14. If u(x,y)= e^x2+y2then ∂u/∂x is equal a) e^x2+y2 b) 2x4 c) x²u                          d) y²
15. 
    
16.  
17. The solution of the differential equation dy/dx=2xy is

a)y=ce ^x2               b)y=2x²+c                   c) y=ce ^-x2                         d)y= x²+c

18. If sinx is the integrating factor of the liner differential equation dy/dx+py, then P a) Log sin x b) cos x                             c) tan x                        d) cot x
19. Let x have a Bernowlli distribution with mean 0.4 than tha variance of        (2x-3)  a) 0.24 b) 0.48                              c) 0.6                     d) 0.96
20. The proposition p^(¬pVq) is a) a tautology b) a contradiction c) logically equivalent to p^q d) logically equivalent to pVq

 

PART-II

Answer any 7 question Q.No-30 Compulsory                                                             7*2=14

21. if adi A= -1    2    2      find A^-1

                         1    1     2

                         2    2     1

22. Find the square root of (6-8i)
23. Prove that a line cannot intersect a circle at more than two points.
24. Find the equation of the ellipse whose focus(±2,0), vertex(±3,0)
25. Show that the vectors i+2j-3k, 2i-j+2k and 3i+j-k are coplanar.
26. Evaluate : lim x log x

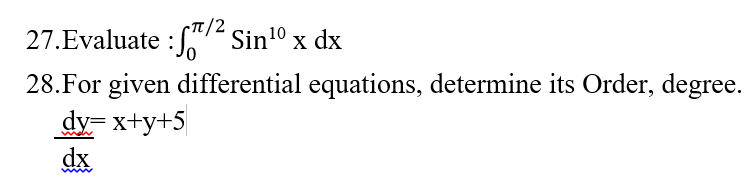
29. Computp(x=k) for binominal distribution B(n,p) where n=6,p=1/3 , k=3
30. In an algebraic structure the inverse of an element(if exists) must be Unique.

 

PART-III

Answer the any 7 question                                                         7*3=21

31. Prove that Cos   -   Sin   is orthogonal

 

                           Sin    -   Cos

32. If |z|=2 show that 3≤|z+3+4i|≤7
33. Form a polynomial equation with integer coefficient with √ as a root
34. Find the principal value of Cosec^-1(-1)
35. The maximum and minimum distances of the Earth from the Sun respectively are 152x10⁶Km and 94.5x10⁶ the sun is at one focus of the elliptical orbit. Find the distance from the sun to the other focus.
36. Find the angle between the straight line

 X+ 3/2 = Y- 1/2 =    -Z

37. Find the angle of intersection of the Curve Y=sin x with the positive x axis.
38. Use liner approximation to find an approximate value of √9.2 without using a calculator
39. Evaluate x⁵(1-x²)⁵ dx
40. Verify the (i) closure property (ii) Commutative Property (iii)associative Property (iv) existence of identify and (v) existence of inverse for the arithmetic operation + on Z₀=the set of all odd integers.

PART-IV

Answer the all questions                                                                  7*5=35

41. a) Investigate for what values of ∂ and µ the system of  liner equations.

x+2y+z=7 , x+y+∂z= µ  , x+3y-5z=5 has (i) no solution (ii) a unique solution (iii)an infinite number of solutions.

(OR)

b) Obtain the Cartesian equation for the locus of Z=x+iy in each of the following cases; |z-4|²-|z-1|²=16

42. a) Slove:6x⁴-35x³+62x²-35x+6 (OR)

      b) Find the centre , foci and eccentricity of the hyperbola 11x²-25y²-44x+50y-256=0

43. a)Prove that sin(α-β)=sinαcosβ-cosα-sinβ (OR)

b)salt is power from a conveyer belt at a rate of 30 cubic meter per minute forming a conical pile with a circular base whose height and diameter of base are always equal. How fast is the height of the pile increasing when the pile is 10 meter high?

45. Slove .+ 2y=e^-x           (OR) b) A random variable X has the following probability mass function find (i)P(2<x<6) (ii) P(2≤<x<5) (iii) p(x≤4) and (iv)P(3<x)
46. Verify Pv(q^ r) = (pvq)^(pvr) (OR) b) On lighting a rocket cracker it gets projected in a parabolic path and reaches a maximum height of 4m When it is 6m away from the point of projection . Finally it reaches the ground 12m away from the starting Point. Find the angle of projection.
47. a)Verify the (i) closure property (ii) commutative property(iii) associative property (iv) existence of identity and (v)existence of inverse for the arithmetic operation _O ^z (OR) b) Find the non-parametric form of vector equation and Cartesian equation of the plane passing through the point (2,3,6) and parallel to the straight lines

 

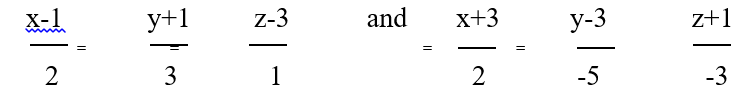
மாதிரி வினாத்தாள் உருவாக்கம்

- ஆசிரியர் சைரா பானு (A3 குழு), 

முதுகலை கணித பட்டதாரி ஆசிரியர், 
அரசு மேல்நிலைப் பள்ளி, 
பொன்னேரி, திருப்பத்தூர்.

இதையும் வாசிக்கலாம்: 12ஆம் வகுப்பு, 10ஆம் வகுப்பு தமிழ், ஆங்கிலம், கணிதம், அறிவியல், சமூக அறிவியல் ஆகிய பாடங்களின் மாதிரி வினாத் தாளைக் காண: https://tamil.abplive.com/topic/question-bank என்ற இணைப்பை க்ளிக் செய்யவும்.